
Establishment of a formula for the estimation of kidney depth in adults and its effect on glomerular filtration rate assessment
Introduction
The glomerular filtration rate (GFR) is a sensitive indicator for evaluating renal function, which can identify abnormal changes in renal function earlier, and can thus be used as an objective indicator to evaluate renal function, especially separate renal function. Inulin or the 51Cr-ethylenediaminetetraacetic acid (51Cr-EDTA) clearance rate are considered to be the gold standard for evaluating the GFR (1); however, the widespread promotion of these is difficult due to their cumbersome operations, numerous influencing factors, and high prices. The biological properties of 99mTc- diethylenetriaminepentaacetic acid (99mTc-DTPA) are similar to those of inulin, and its clearance in the body is well correlated with the clearance of 51Cr-EDTA (2). The 99mTc-DTPA renal dynamic imaging method, also known as Gates’ analysis method, is used to measure both the total kidney GFR and the GFR of the left and right kidneys separated. It has become a routine examination method for clinical evaluation of total kidney and separated kidney function. At present, when Gates’ analysis method is used to calculate the GFR, the Tønnesen’s formula (3), which is obtained by B-ultrasound measurement, is applied to estimate the kidney depth (KD). Gates’ analysis method posits that the influence of KD on the GFR is more important than that of other factors (4).
Several methods, including B-ultrasound, computed tomography (CT), and the radionuclide lateral imaging technique, are currently used for KD measurement. Among these, the CT measurement method is more accurate than B-ultrasound (5) and radionuclide lateral imaging (6). To estimate the KD, several formulas are commonly used: Tønnesen’s formula (3), Taylor’s formula (7), Li Q’s formula (8), Ma G’s formula (9), Uchiyama’s formula (10), and Xue JJ’s formula (11), which was obtained in our previous study. The KD results obtained by various estimation formulas differ. Tønnesen’s formula underestimates the KD and the corresponding GFR, which is a matter of consensus among scholars (12). Taylor’s formula was established using European and American populations, and its accuracy for Chinese KD measurement remains controversial (8,11). Li et al. (8) proposed the Li Q’s formula, which was the first to be established in Chinese populations and has been verified by other researchers (8,13). However, they also proposed that the degree of fat aggregation differs with age, which affects the KD and in turn affects the GFR under certain conditions. The Ma G’s and Uchiyama’s formulas are based on the above parameters, adding body thickness (T) to fit the estimation formula for calculating the KD and obtaining better clinical results (9,10).
Gates’ analysis method is the only method to determine the GFR of the kidney in clinical practice (4) and is recommended for the determination of GFR in kidney transplantation (14). There are strict requirements for the donor kidney GFR during kidney transplantation (15). Although CT measurement of the donor KD can improve the accuracy of the GFR measured by the Gates’ analysis method, it will increase the radiation exposure of kidney transplantation donors. To obtain a more accurate GFR of the total (both) and separate (left and right) kidneys for the general population and avoid unnecessary radiation exposure, it is particularly important to establish an empirical formula for KD that is more consistent with the real KD.
In this study, healthy transplanted kidney donors were used as the research object, and the CT-measured KD and the corresponding GFR were used as the standard to fit the empirical formula to the KD and its related factors (gender, age, height, weight, body thickness).The obtained formula was then compared with the KD estimated by the above formulas and the corresponding GFR to determine an empirical formula for KD that can replace the actual measured KD by CT and is suitable for the general population in China. We present the following article in accordance with the MDAR reporting checklist (available at https://tau.amegroups.com/article/view/10.21037/tau-22-614/rc).
Methods
Research subjects
In total, 326 healthy renal transplantation donors who underwent preoperative renal dynamic imaging in The First Affiliated Hospital of Xi’an Jiaotong University from October 2011 to December 2017 were collected for further analysis. Among these patients, the male-to-female ratio was 1:1.94 (males: 111 vs. females: 215) and the average age was (49.35±7.21) years old (range, 23–65 years). Next, the cohort was randomly divided into a fitting formula training group (167 cases) and a formula validation group (159 cases). A total of 127 cases were selected from the formula validation group as the GFR measurement group who received routine renal dynamic imaging, including 36 males and 91 females with an average age of (49.2±7.32) years old (range, 23–64 years).
All of the renal transplant donors were in good health, had no history of kidney disease or trauma, and did not suffer from hypertension or diabetes. Before the examination, routine preoperative examinations were carried out, including electrocardiogram (ECG), blood pressure, routine blood test, routine urine test, liver and kidney function examinations, blood glucose level assessment, liver and kidney ultrasound, and donor-receptor tissue matching. All candidates were normal and met the kidney donor criteria. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the institutional review board (No. XJTU1AF2022LSK-376) at The First Affiliated Hospital of Xi’an Jiaotong University (Xi’an, China) and individual consent for this retrospective analysis was waived.
KD regression formula
Multivariate linear regression analysis was used to establish an empirical formula for calculating the KD based on data of the 167 fitting formula training set cases with multiple variables, including gender, age, height (H, cm), weight (W, cm), body mass index (BMI), body thickness (T, cm).
KD measurement by CT scanning
KD was measured using a Symbia T16 single-photon emission computed tomography (SPECT)/CT scanner (Siemens, Berlin, Germany). The acquisition conditions were as follows: tube rotation speed, 0.4 s/r; scanning thickness, 0.5 mm; reconstruction thickness, 1mm; field of view, 280–300 mm; tube voltage, 120–135 kv; and tube current, 200mA. The patients were placed in the supine position and held their breath during the scan. The CT scan ranged from the top of the liver to the level of the iliac spine. The T and KD calculations are shown in Figure 1 (16).
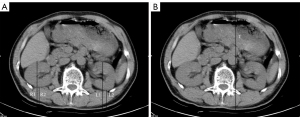
GFR measurement by SPECT renal dynamic imaging
A Symbia T16 SPECT/CT scanner (Siemens) was used to perform 99mTc-DTPA renal dynamic imaging to measure the GFR of the total kidney and sub-renal. The acquisition conditions were as follows: low energy general collimator; peak, 140 KeV; and window width, ±20%. After placement in the supine position, the probe post vision, including the lower abdomen and pelvic area, was aimed at the double renal region. An intravenous “projectile” injection [111–185 MBq (3–5 mCi) and radiochemical purification >95% 99mTc-DTPA, volume <1 mL] was administered.
When the abdominal aorta is developed, the switch was activated to dynamically collect, blood flow Phase 1 frame/2 s, collect 32 frames, function Phase 1 frame/30 s, collect 32 frames, and a total of 20 min. Patients were required to drink 300–500 mL of water 30 minutes and urinate before the examination. Also, data including gender, age, height, weight, and BMI were recorded.
Image analysis
According to the Symbia T16 SPECT/CT processing procedure, the kidneys and background region of interest (ROI) were drawn on the kidneys and lower edges of the kidneys. Using the SPECT/CT built-in software, the workstation automatically displayed the KD calculated by Tønnesen’s formula and the kidney GFR value calculated by Gates’ method. Keeping the radioactivity count before injection, radioactivity after syringe, kidney and ROI unchanged, the KD was estimated by CT measurement and six formulas. Based on Gates’ analytic formula, the routine processing program of the computer was used to generate the double kidney time-radioactivity curve (kidney chart) as well as the corresponding left and right kidney and total kidney GFR values.
Statistical analysis
SPSS 18.0 software (Chicago, USA) was used for statistical analysis. Multiple linear regression analysis was used to fit the formula for estimating KD. Each formula was used to estimate the GFR of the left and right KD in the formula verification and GFR measurement groups. The results were expressed as the mean ± standard deviation (), and Pearson analysis was used to estimate the correlation between different formulas. The accuracy of our formula was estimated by the rank-sum test. P<0.05 was considered to indicate a statistically significant difference.
Results
KD regression formula
Based on the clinical data of the training set, the fitting formula for KD was analyzed and calculated using a multivariate linear regression model, which was listed as follows:
KDL: Dl (cm)=7.148011×W/H+0.185258×T+0.283907
KDR: Dl (cm)=0.044754×W+0.171129×T+0.689078
where W is weight (kg), H is height (cm), and T is body thickness (cm).
The results showed that the factors affecting the KD were weight, height, and body thickness, and gender and age did not affect the prediction of KD. The general information of the fitting formula group is shown in Table 1.
Table 1
| Variable | n | Mean ± SD | Range |
|---|---|---|---|
| Gender | |||
| Male | 57 | – | – |
| Female | 110 | – | – |
| Age (years) | 167 | 49.1±7.17 | 26–65 |
| Height (cm) | 167 | 163.8±6.47 | 150–180 |
| Body weight (kg) | 167 | 62.5±8.43 | 45–87 |
| BMI (kg/m2) | 167 | 23.2±2.65 | 16.9–30.4 |
| Body thickness (cm) | 167 | 21.3±2.54 | 14.7–29.5 |
BMI, body mass index.
Comparison between the estimated KD of each formula and the actual CT measurement
Comparison and analysis results between the measured KD by CT and the estimation formulas
The KDs measured by CT, the five previous empirical formulas, and the fitting formula in this study are shown in Table 2.
Table 2
| Formula | KDL (cm) | KDR (cm) | Z (Left/Right) | P (Left/Right) |
|---|---|---|---|---|
| CT-measured KD | 6.99±1.14 | 7.24±1.15 | − | − |
| Fitting formula | 7.05±0.718 | 7.21±0.748 | −1.56/−0.219 | 0.118/0.826 |
| Taylor’s formula | 6.52±0.774* | 6.89±0.720* | −5.61/−4.31 | 0.000/0.000 |
| Li Q’s formula | 7.08±0.783 | 7.11±0.721 | −1.42/−1.65 | 0.156/0.099 |
| Ma G’s formula | 7.08±0.809* | 7.41±0.820* | −1.99/−2.72 | 0.047/0.007 |
| Uchiyama’s formula | 7.78±0.831* | 7.93±0.768* | −8.81/−8.19 | 0.000/0.000 |
| Xue JJ’s formula | 6.78±0.679 | 7.03±0.685 | −1.70/−1.36 | 0.089/0.175 |
*P<0.05, compared with the CT-measured KD. CT, computed tomography; KD, kidney depth.
The fitting, Li Q, and Xue JJ formulas in this study were not statistically different from the CT-measured KD (P>0.05). Meanwhile, the Taylor, Ma G, and Uchiyama formulas were markedly different from the CT-measured KD (P<0.05).
Correlation analysis of KD among estimation formulas
There was a positive correlation between the CT measurements and the depth of the left and right kidneys in all empirical formulas (P<0.01), as shown in Figure 2.
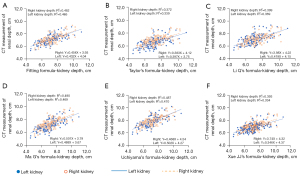
The correlation coefficients r of the KDL/KDR between the fitting formula in this study and the Taylor, Li Q, Ma G, Uchiyama, and Xue JJ formulas were 0.917/0.931, 0.937/0.940, 0.999/0.987, 0.997/0.988, and 0.900/0.945, respectively.
The correlation coefficient r of the KDL/KDR between Xue JJ’s formula and the Taylor, Li Q, Ma G, and Uchiyama formulas were 0.946/0.971, 0.956/0.980, 0.882/0.918, and 0.872/0.932, respectively.
Comparison of the GFR measured by CT and estimated by the various formulas
Comparison and analysis results between the measured GFR by CT and the estimation formulas
In this study, the CT-measured KD, five empirical formulas, and the fitting formula were used to estimate the KD of the GFR measurement group, and Gates’ analysis was adopted to calculate the GFRL and GFRR corresponding to each KD, as shown in Table 3.
Table 3
| Formula | GFRL (mL/min) | GFRR (mL/min) | Z (Left/Right) | P (Left/Right) |
|---|---|---|---|---|
| CT measurement GFR | 47.8±10.8 | 48.5±11.0 | – | – |
| Fitting formula | 47.4±8.91 | 47.3±8.97 | −0.081/−1.33 | 0.936/0.184 |
| Taylor’s formula | 43.4±8.39* | 44.8±8.37* | −5.55/−4.88 | 0.000/0.000 |
| Li Q’s formula | 47.6±9.20 | 46.6±8.69* | −0.056/−2.42 | 0.955/0.016 |
| Ma G’s formula | 47.7±9.04 | 49.0±9.43 | −0.562/−1.53 | 0.574/0.127 |
| Uchiyama’s formula | 53.4±10.2* | 53.3±10.0* | −7.05/−6.77 | 0.000/0.000 |
| Xue JJ’s formula | 45.1±8.64 | 46.0±8.51 | −1.65/−1.40 | 0.098/0.160 |
*P<0.05, compared with the CT-measured GFR. GFR, glomerular filtration rate; CT, computed tomography.
There was no significant difference in the GFRL and GFRR corresponding to the measured KD on CT with that corresponding to the fitting formula of this study as well as the Ma G’s and Xue JJ’s formulas (P>0.05). Also, there was no notable difference in the GFR value corresponding to Li Q’s formula in the left kidney (P>0.05); however, the right kidney exhibited a marked difference (P<0.05).
The GFRL and GFRR calculated by Taylor’s formula were all lower than those calculated by the CT-measured KD (P<0.05), while the GFRL and GFRR calculated by Uchiyama’s formula were higher than those calculated using the CT-measured KD (P<0.05).
Correlation analysis of the GFR values corresponding to computed KD estimated between CT measurement and the various estimation formulas
We observed a positive correlation between the GFRL and GFRR corresponding to the KD measured by CT (P<0.01), as shown in Figure 3.
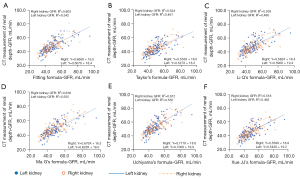
In this study, the fitting, Ma G, and Uchiyama formulas exhibited the best correlation with the GFR value corresponding to the CT-measured KD, and the predicted GFRR was better than GFRL.
Discussion
At present, 99mTc-DTPA renal dynamic imaging is the only method that can quantitatively detect the total and separated renal GFRs. Gates’ analysis is based on renal dynamic imaging, and Gates (4) believed that KD is the most important factor affecting the GFR results. The present study showed that there was no significant difference between the KD estimated by the Xue JJ’s formula and that measured by CT as well as the corresponding GFRs of the left and right kidneys (P>0.05), indicating that the Xue JJ’s formula can reflect the KD estimated by CT and the corresponding GFRs of left and right kidneys for Chinese adults. It can replace the CT measurement of KD to calculate the GFR and is easily adopted in clinical practice. With only the patient’s height and weight, a more accurate KD can be obtained, which highlights the accuracy of Xue JJ’s formula for KD estimation in Chinese adults as well as the corresponding GFRs of the left and right kidneys. However, the Xue JJ’s formula still needs more clinical data to verify its accuracy, so at this stage, the Xue JJ’s formula is only used for the estimation and verification of the KD in our local service area. This study further confirmed the accuracy of the Xue JJ’s formula in estimating renal depth and calculating GFR, and provided a basis for further clinical applications. Some people believe that Taylor’s formula was established using European and American populations, which may not apply to the Oriental races. Yang et al. (13) showed that the Li Q’s formula is better than Taylor’s formula and is suitable for estimating the KD of Chinese individuals. In this study, we compared the KD and GFR and found that there was no significant difference between the KD measured by the Li Q’s formula and CT, both of which were higher than the KD and GFR obtained by the Taylor’s formula. This supported the perspective of Yang et al., and also demonstrated that the GFR difference was caused by the difference in KD. The present study also illustrated that there was no significant difference in the GFRL corresponding to the KDL and KDR estimated by the Li Q’s formula (P>0.05), whereas the GFRR exhibited a notable difference (P<0.05), indicating that minor changes in the KD lead to marked differences in the GFR. Therefore, CT measurement of KD can improve the accuracy of GFR calculations. This is especially true for living kidney transplant donors who need accurate renal GFR partitioning (17,18).
Uchiyama et al. (10) measured the body thickness at the renal hilum level by CT and introduced it into the renal depth estimation formula, believing that body thickness was the biggest factor affecting the KD. This viewpoint was also confirmed by Ma et al. (9). The present study found that the correlation between Uchiyama’s formula, Ma G’s formula, and the fitting formula of this study and the CT-measured KD and corresponding GFR was significantly stronger than that of the Taylor, Li Q, and Xue JJ formulas without the inclusion of body thickness, and the predicted GFRR was better than GFRL, indicating that body thickness was also the main factor affecting GFR. At the same time, it is suggested that the fitting formula based on the same parameters exhibits a good linear correlation; that is, theoretically, the fitting, Ma G, and Uchiyama formulas in this study were superior to the other estimation formulas. Moreover, errors in KD caused by age difference and changes in fat accumulation can be excluded (9). Therefore, the calculated GFR is closer to the GFR corresponding to the CT-measured KD.
The results of this study also showed that the KDL and KDR estimated by Uchiyama’s formula had the best correlation with that measured by CT (0.470/0.487); however, there were significant differences in the KD and GFR measured by Uchiyama’s formula and CT (P<0.05). Two factors may explain this difference. Firstly, KD has a significant effect on GFR estimation, and small differences in KD can lead to considerable GFR changes. Secondly, the two methods established population differences in the impact of race on KD and GFR (8). The KDs estimated by the two methods in this study were consistent with the correlation and accuracy of their calculation of the GFR, which may indicate that Uchiyama’s formula is suitable for the estimation of KD and the corresponding GFR in Japanese people, but is not necessarily suitable for Chinese people and may overestimate the KD measured by real CT and its corresponding GFR.
This study also showed that there was a significant difference between Ma G’s formula and CT measurement in KD (P<0.05). However, no notable difference in the GFR value of the left and right kidneys was observed (P>0.05). The inconsistent KD and its corresponding GFR may be caused by other factors other than the KD. Studies have shown that age influences the KD and GFR (7,19). Ma G’s formula is suitable for the estimation of KD in adults and children. Children accounted for almost 30% of their study population, which is a special group exhibiting continuous growth and development. Before the age of 2 years, there are substantial differences in kidney development and GFR growth with age. However, after the age of 2 years, GFR tends to be stable. Zhao et al. (20) established the reference range of normal GFR for Chinese children <12 years old: 8 weeks–1 year old, 50–90 mL/min; 1–2 years old, 67–91 mL/min; 2–3 years old, 75–95 mL/min; 3–10 years old, 72–96 mL/min; and 10–12 years old, 72–100 mL/min. The reference value of the total GFR of normal adults is 90–120 mL/min/1.73 m2. In general, the GFR decreases by about 4 mL/min/1.73 m2 every 10 years before the age of 50 years. The decline in GFR accelerates significantly after the age of 50 years, and the GFR decreases by about 10 mL/min/1.73 m2 every 10 years (19). The difference in GFR between children and adults may lead to an insignificant difference in the corresponding GFR even if there is a difference in KD, indicating that the change in children’s KD is more obvious relative to its GFR. Therefore, KD estimation for children and adults should be calculated separately; a special formula should be established for estimating KD in children to facilitate the GFR determination by Gates’ analysis.
The findings of the present study also showed that the fitting formula with CT-measured KD and GFR values corresponding to the left/right kidney were not significantly different (P>0.05). Compared with the KD estimated by Xue JJ’s formula, the GFRL and GFRR calculated in our study were closer to the CT-measured values. This indicated that the KD estimated by the current fitting formula in this study and the corresponding GFRL and GFRR were more consistent with that calculated by the CT-measured KD, which is superior to Xue JJ’s formula. However, the deficiency of the fitting formula of this study is that it cannot accurately measure body thickness, so its clinical application for calculating the GFR is limited. The fitting formula of this study can play a more significant role if an accurate measurement method of the body thickness at the level of the hilum on the body surface can be established.
In conclusion, Xue JJ’s formula could replace CT measurement of KD and the corresponding GFR for the general Chinese adult population, and its application in clinical practice is easy. The fitting formula of this study can play a more important role if an accurate measurement method of the body thickness at the level of the hilum on the body surface can be established.
However, this study also had some deficiencies that should be noted. Firstly, although KD is the main factor influencing Gates’ GFR measurement, there are other factors, such as hydration status and background selection (21), which can also affect the GFR measured by Gates’ method and needs further investigation. Secondly, this study only reflects the relationship between KD and GFR at a certain age. However, this study also fully demonstrated that Xue JJ’s formula has the advantages of accuracy and convenience in calculating the kidney GFR value in the Chinese population, and is worthy of promotion.
Acknowledgments
Funding: None.
Footnote
Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at https://tau.amegroups.com/article/view/10.21037/tau-22-614/rc
Data Sharing Statement: Available at https://tau.amegroups.com/article/view/10.21037/tau-22-614/dss
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://tau.amegroups.com/article/view/10.21037/tau-22-614/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the institutional review board (No. XJTU1AF2022LSK-376) at The First Affiliated Hospital of Xi’an Jiaotong University (Xi’an, China) and individual consent for this retrospective analysis was waived.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Godfrey T, Cuadrado MJ, Fofi C, et al. Chromium-51 ethylenediamine tetraacetic acid glomerular filtration rate: a better predictor than glomerular filtration rate calculated by the Cockcroft-Gault formula for renal involvement in systemic lupus erythematosus patients. Rheumatology (Oxford) 2001;40:324-8. [Crossref] [PubMed]
- Petersen LJ, Petersen JR, Talleruphuus U, et al. Glomerular filtration rate estimated from the uptake phase of 99mTc-DTPA renography in chronic renal failure. Nephrol Dial Transplant 1999;14:1673-8. [Crossref] [PubMed]
- Schlegel JU, Hamway SA. Individual renal plasma flow determination in 2 minutes. J Urol 1976;116:282-5. [Crossref] [PubMed]
- Gates GF. Glomerular filtration rate: estimation from fractional renal accumulation of 99mTc-DTPA (stannous). AJR Am J Roentgenol 1982;138:565-70. [Crossref] [PubMed]
- Granerus G, Moonen M. Effects of extra-renal background subtraction and kidney depth correction in the measurement of GFR by gamma camera renography. Nucl Med Commun 1991;12:519-27. [Crossref] [PubMed]
- Maneval DC, Magill HL, Cypess AM, et al. Measurement of skin-to-kidney distance in children: implications for quantitative renography. J Nucl Med 1990;31:287-91. [PubMed]
- Taylor A, Lewis C, Giacometti A, et al. Improved formulas for the estimation of renal depth in adults. J Nucl Med 1993;34:1766-9. [PubMed]
- Li Q, Zhang CL, Fu ZL, et al. Measuring kidney depth of Chinese people with kidney dynamic imaging. Chinese Journal of Medical Imaging Technology 2007;23:288-91.
- Ma G, Shao M, Xu B, et al. Establish New Formulas for the Calculation of Renal Depth in Both Children and Adults. Clin Nucl Med 2015;40:e357-62. [Crossref] [PubMed]
- Uchiyama K, Kuniyasu Y, Niio Y, et al. Proposal on new formulas for renal depth in the technetium-99m-mercaptoacetyltriglycine (MAG3) scintigraphy. Kaku Igaku 1997;34:159-66. [PubMed]
- Xue J, Deng H, Jia X, et al. Establishing a new formula for estimating renal depth in a Chinese adult population. Medicine (Baltimore) 2017;96:e5940. [Crossref] [PubMed]
- Liu Y, Zhao AM, Lu XN, et al. Measurement of glomerular filtration rate in living donor kidney by Gates method with computed tomography. Chinese Journal of Organ Transplantation 2019;40:195-9.
- Yang H, Li Q, Li W, et al. Applicability of three formulas in measuring renal depth of Chinese people. Chinese Journal of Medical Imaging 2013;21:652-5.
- Branch of Organ Transplantation of Chinese Medical Association, Branch of Organ Transplant Physician of Chinese Medical Doctor Association. Clinical guideline on living donor renal transplantation in China (2016 Edition). Organ Transplantation 2016;7:417-6.
- Garg N, Poggio ED, Mandelbrot D. The Evaluation of Kidney Function in Living Kidney Donor Candidates. Kidney360 2021;2:1523-30. [Crossref] [PubMed]
- Knight EL, Verhave JC, Spiegelman D, et al. Factors influencing serum cystatin C levels other than renal function and the impact on renal function measurement. Kidney Int 2004;65:1416-21. [Crossref] [PubMed]
- Kim SH. Effects of Changes in Analytic Variables and Contrast Material on Measurement of Computed Tomography Glomerular Filtration Rates in Healthy Candidates. J Comput Assist Tomogr 2020;44:217-22. [Crossref] [PubMed]
- Gaillard F, Jacquemont L, Lazareth H, et al. Living kidney donor evaluation for all candidates with normal estimated GFR for age. Transpl Int 2021;34:1123-33. [Crossref] [PubMed]
- Granerus G, Aurell M. Reference values for 51Cr-EDTA clearance as a measure of glomerular filtration rate. Scand J Clin Lab Invest 1981;41:611-6. [Crossref] [PubMed]
- Zhao XF, Zhao RF, Ruan SS, et al. Establishment and calibration of normal reference intervals for GFR of the healthy children with99m Tc-DTPA renal dynamic imaging. Journal of Clinical Pediatric Surgery 2015;14:33-36.
- Durand E, Prigent A. The basics of renal imaging and function studies. Q J Nucl Med 2002;46:249-67. [PubMed]


